今日は、カオスについて遊べるサイトを紹介します。
ローレンツアトラクターというのをご存知ですか。こちらのサイトをChromeなどでひらいてみると(Firefoxではなぜか青いバタフライが飛びません)、ローレンツアトラクタをいろいろな条件で試して遊んでみることができます。
http://www.malinc.se/m/Lorenz.php
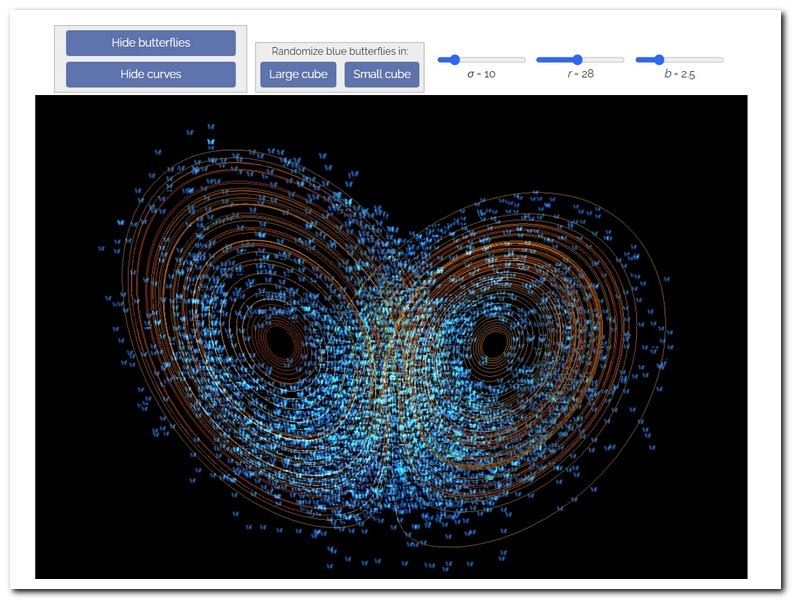
もともとはアメリカの気象学者Lorenzが大気の対流運動を記述するために研究していた連立微分方程式で以下の式です。温度差による大気の上昇・下降の流れや、地球の回転によるコリオリ力など、大気の複雑な挙動を捉えるための非線形連立微分方程式でした。
dx/dt = σ(y – x)
dy/dt = x(r – z) – y
dz/dt = xy – bz
で記述される点(x,y,z)の時間変化が解になります。σとrとbがパラメーターで、このサイトの上部にあるパラメータをスライダで変化させると、カオスのアトラクタが現れたり、消えたりします。ページを開いた時のデフォルト値はσ=10 r=28 b=2.5になっており、Small cubeボタンかLarge cubeボタンのどちらかを押してsimulationをはじめると、はじめ近くにあった青色のバタフライが時間とともに運動をはじめて、時間がたつと羽根をひらいた蝶のような形の軌道にそって運動するようになることがわかります。それぞれの青色のバタフライは、微分方程式を満たすように運動しているだけですが、この場合、周期性はまったくない運動となります。すべての解が時間がたつと羽根を広げた蝶々のような空間の領域に分布する様子がよくわかります。アトラクタというのはこういう解の点が一定の領域に集中することからついた名前です。ローレンツアトラクタがあらわれるのは、σ=10 b=3/8の場合、r>24.74の場合で、ごく近くにあった二つの点の運動を上記の連立微分方程式系で計算すると、まったく異なるカオスの振る舞いをすることになります。上のサイトでいろいろ試してみてください。
サイトのHide butterflyボタンを押した場合は、二つの点の運動の軌跡が表示されます。

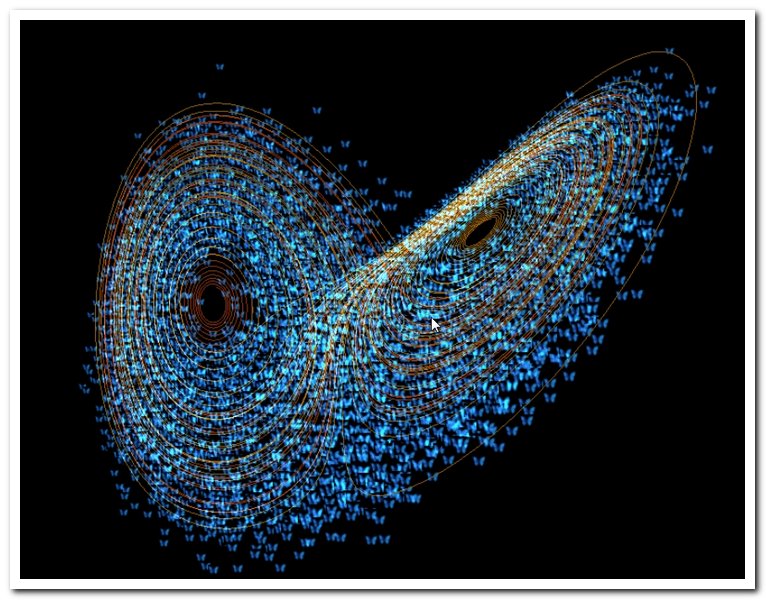
また、図の上にマウスをおいてドラッグすると図形全体を回転させたりできるので、三次元空間でのローレンスアトラクタの形を詳しく観察することもできます。
カオスについては以下の英語の動画もわかりやすいのでお勧めです。
Chaos: The Science of the Butterfly Effect
https://youtu.be/fDek6cYijxI