高校生に知ってほしい強力ツール ベンゼンの異性体を描いてみよう！：化学式から異性体の構造（環や二重結合、三重結合の存在可能性）を推定する方法
今年も残すところあと一日となりました。今年の福岡はことのほか紅葉がきれいで長く続きました。写真は11月に大宰府近くにある竈門神社(かまどじんじゃ)に行った時に境内で撮影した紅葉です。青空に映えてとてもきれいでした。
さて、今日は一足早いお年玉ということで、有機化学を学び始めた高校生や受験生、一般の方々に是非覚えておいてほしい強力なツールを紹介します。試験問題を解くのにも大活躍しますので、活用してみてください。
先日のブログで、三炭糖のdihydroxylacetoneが隕石の中から発見されているというお話をしました。C3H6O3という分子式で示される物質がどのような構造をしているかを推定する簡単な方法を紹介します。これは有機化合物の構造を質量スペクトルやNMRなどで推定する際に常用される方法です。（たとえば「有機化合物のスペクトルによる同定法 (第8版)」(東京化学同人）をご覧ください）
分子式はその物質がどのような元素からなり、それぞれの元素が何個あるかという情報の他に、分子内にある環や不飽和結合(二重結合や三重結合）の数についても教えてくれるのです。不飽和結合の存在や環の存在によって結合している水素の数が、環や不飽和結合がない場合にくらべてどれくらい減っているかを示すhydrogen deficiency indexという数を分子式から計算することができます。このインデックス（数）を計算すると、分子式内の二重結合の数、三重結合の数の二倍の数、および環状構造の個数の合計がわかります。計算の仕方は以下のとおりです。
hydrogen deficiency index=（炭素数＋１）ー水素数/2ーハロゲン数/2＋三価の窒素数/2です。
たとえばC3H6O3（つまり炭水化物C3(H2O)3の場合）なら、上の式で炭素数3、水素数6、酸素数3なので、（3+1）-6/2ということで1がインデックスとなります。つまりこの分子式で表される分子には二重結合が1個あるか、または環が一個あるだろうと予測できるわけです。ケトースもアルドースもありうることがわかりますね。
C7H7NOの場合だと、炭素原子数が7、水素が7、窒素が一個で酸素が1個ですので、インデックスは（7+1）-7/2+1/2となり、5となります。この分子はたとえばベンズアミドでありうるわけです。ベンゼン環には二重結合3つ、環が一個ありますからそれだけで4となりあとはアミド結合の酸素と炭素の間の二重結合が1となり合計5になります。この分子式でインデックスが５になるような異性体を練習に書いてみてください。
簡単な練習としてはC6H6が面白いです。良く知られているのはベンゼンです。しかしこの化学式で示される分子はもっといろんなものがあり得ます。
C6H6という分子のインデックスは炭素6個に水素6個ですから、（6+1）-6/2で4です。ベンゼンなら環が1個で二重結合3個ですのでたしかに4となってあっています。しかし環が1個で三重結合が1個(1x 2=2)、二重結合が1個でも4ですよね。大学生のときこのインデクスを使ってものすごい数の構造異性体を書いて遊んでいたのを思い出します。うちの奥さんが地味な遊びや、といっている声が聞こえますが‥‥。
解答例をはりつけておきます。もっといろいろ(合計30種類以上）書けますので試してみてください。(図は、ChemSpider(無料の化学構造のデータベースで、テキスト検索や構造検索ができます）という便利な化学のサイトで分子式C6H6の異性体を検索した結果から、一部を抜き出して、図を改変したものです。もとのページを見たい方はこちらです。）
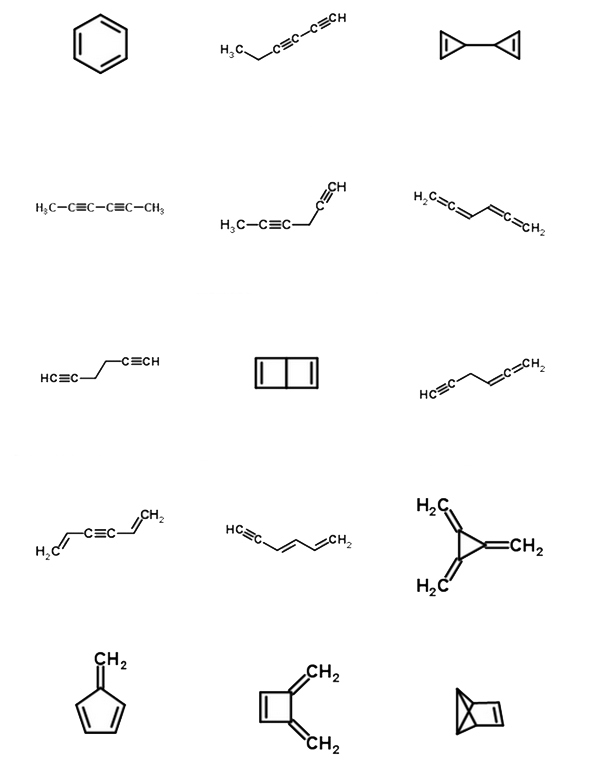
もっと一般化したインデックスの計算式は以下のようになります。
hydrogen deficiency index =(Ⅳ)+1-（Ⅰ/2）+（Ⅲ/2）
ここでⅣというのは４価の元素(炭素Cとかケイ素Siの原子の数）
Ⅰは一価の元素の数、つまり水素Hやハロゲン(ClとかFとか）の原子数の合計
Ⅲは三価の元素の原子の数、つまり窒素Nとかリン原子Pなどの数です。
下の写真は竈門神社本殿そばの池に浮かんでいた もみじの落ち葉です。ゆっくりと風にふかれて水面をただよっていました。
